报告题目：Invariant manifolds for a randomly perturbed non-autonomous coupled system and their approximations

主讲人：申俊

单位：四川大学数学学院

时间：8月17日 15:00

地点：学院南研

摘要：In thistalkweconsiderlong time dynamics of a randomly perturbed non-autonomous coupled system (x,y), whose x coordinate satisfies a semilinear parabolic equation with an additive noise, and y coordinate satisfies a differential equation whose solutions do not converge too rapidly. The noise is either the white noise induced by a Brownian motion W(t,w)or a stationary process 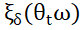 whose integral is approximating. After addressing W(t,w) certain assumptions for such system, we show that for 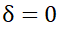  (resp. 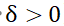 ) with respect to the noise W(t,w) (resp. integral of 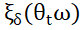  there exists a invariant manifold which is exponentially attracting any other solution outside it. Also, as tends to 0, the invariant manifold and its derivative in for the case 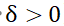 are approaching to those for  .

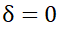简介：申俊，四川大学副教授，博士生导师,四川省学术和技术带头人后备人选；曾在英国伦敦帝国理工学院、美国杨百翰大学访问；现主持国家自然科学基金面上项目1项，参加国家重大、重点项目各1项；在《Journal of Differential Equations》、《Journal of Dynamics and Differential Equations》、《Discrete and Continuous Dynamical Systems-Series A》、《SCIENCE CHINA Mathematics》、《Physica D》等上面发表文章数篇。